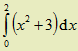pomocí obdélníkové metody s přesností lepší než 0,01. Srovnejte získanou hodnotu s hodnotou vypočtenou pomocí primitivní funkce.
3.8 Numerický výpočet určitých integrálů
Mnoho funkcí, s nimiž se setkáváme v přírodovědných a technických aplikacích, nelze integrovat jednoduchými analytickými metodami jako je například substituce nebo metoda per partes. V některých případech dokonce nelze vůbec nalézt primitivní funci ve formě výrazu sestávajícího z elementárních funkcí. Při výpočtu takových integrálů se obvykle uchylujeme k numerickým metodám. Ústřední myšlenka numerického přístupu spočívá v náhradě integrované funkce funkcí jinou, zpravidla mnohem jednodušší, kterou již integrovat umíme. Přibližnou náhradou se pochopitelně dopouštíme chyby, kterou však většinou umíme učinit zanedbatelně malou.
Teorii naleznete v kapitole 6.6.4 Multimediální encyklopedie nebo v kapitole 3.8 Breviáře
Příklad 1
Spočtěte určitý integrál 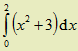pomocí obdélníkové metody s přesností lepší než 0,01. Srovnejte získanou hodnotu s hodnotou vypočtenou pomocí primitivní funkce.
Řešení
Obdélníková metoda spočívá v nahrazení funkce konstantou. Použijeme kombinaci dvou obdélníkových metod, které volí tuto konstantu rovnou funkční hodnotě v levé, resp. pravé hranici daného intervalu.
Nahradíme-li funkci v libovolném intervalu <a,b> konstanou K , můžeme snadno spočítat určitý inegrál v těchto mezích jako obsah obdélníka se stranami (b-a) a K.
(I když je určení primitivní funkce triviální, pro názornost použijme v Mathematice funkci Integrate k určení primitivní funkce, potažmo neurčitého integrálu)
Určitý integrál lze s pomocí této primitivní funkce určit jako rozdíl jejích hodnot v obou krajních bodech intervalu.
Tedy skutečně obsah příslušného obdélníka. Protože určitý integrál má význam obsahu plochy pod křivkou (grafem funkce), znaméná to, že hodnotu této plochy nahrazujeme hodnotou plochy obdélníka. Vraťme se k našemu výpočtu.
(Definujme nejdříve naši funkci a obě meze)
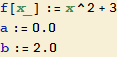
Zkusme nejdříve nahradit hodnotu funkce v celém intervalu daném mezemi integrace a a b konstantou f(a), resp. f(b). V tom případě máme dva obdélníky představující dolní a horní odhad určitého integrálu.
Jako horní odhad chyby výpočtu můžeme brát rozdíl obou hodnot
To je mnohem více než žádaných 0,01.
Dá se ale očekávat, že při rozdělení intervalu <a,b> na větší počet menších intervalů, přičemž v každém z nich bude funkce opět nahrazena konstantou rovné funkční hodnotě levé, resp. pravé meze, bude chyba menší. Naše funkce je rostoucí, proto v každém z těchto intervalů bude hodnota plochy obdélníka vždy pod, resp. nad hodnotou určitého integrálu v tomto intervalu. Součet ploch všech obdélníků pak reprezentuje horní, resp. dolní odhad našeho integrálu v mezích a a b.
Při rozdělení na n intervalů tedy platí pro šířku každého z nich
Pro polohu levých, resp. pravých mezí k-teho intervalu (hodnota k jde od 1 do n) platí:
Dolní, resp. horní odhad je reprezentován součty (součty ploch obdélníků) - (pro součet lze použít funkci Sum):
Zvolme například n=10. Potom
Jako horní odhad chyby výpočtu máme
To je stále více než bylo požadováno
Zvolme n=1000. Potom
Horní odhad chyby výpočtu je tedy
Při rozdělení integrační oblasti na 1000 intervalů již máme požadovanou přesnost (menší než 0,01) zaručenu.
Ověme to srovnáním s přímým výpočtem pomocí primitivní funkce k naší integrované funkci.
(V Mathematice použijeme opět funkci Integrate, ovšem s doplněním mezí integrace a a b)
Odchylky obou odhadů (tj. hodnot z numerických výpočtů).
Vidíme, že oba odhady se v rámci požadované přesnosti shodují s "přesným výsledkem", tj. hodnotou získanou po dosazení mezí (uvozovky jsou zde proto, že získání této hodnoty je spojeno s výpočtem prostřednictvím čísel v desetinném vyjádření, který je rovněž řešen numericky a tedy zatížen numerickou chybou - z tohoto pohledu je náš numerický vypočtený integrál rovnoceným výsledkem).
(Mathematica umožňuje provést i přímo takový numerický výpočet integrálu, a to pomocí funkce NIntegrate )
(V Mathematice je přednastavena dostatečně velká přesnost spočtení a výpisu výsledků, obě přesnosti lze nastavit pomocí funkcí WorkingPrecision a WritingPrecision)
